比较:pytorch和sklearn的比较
| 功能 | 使用 |
|---|---|
| 输出tensor的形状 | tensor.shape |
| 输出tensor的维度 | tensor.dim() |
| 张量所有元素除以一个数 | torch.div(tensor, val) |
view()的作用相当于numpy中的reshape,重新定义矩阵的形状。view前后的元素个数要相同。
torch.arange(1,10) #产生 1~9 组成的一维张量,第一个值缺省就从0开始
view中一个参数定为-1,代表动态调整这个维度上的元素个数,以保证元素的总数不变。
交换输入张量 input 的两个维度
torch.transpose(x, 0, 1) #这就是把x矩阵的0维和1维度交换,即转置
torch.transpose(x, 1, 0) #这个和上面的是一样
torch.transpose(x, -2, -1) #这个将最后一个维度和倒数第二个维度交换,比如有一个张量为[3x4x5],那么执行转换以后变为[3x5x4]
squeeze:降维,将维度为1的去掉,比如[3x1x4x1x5]执行tensor.squeeze(),变为[3x4x5]
t = torch.full([3,1,4,1,5], 5)
t.squeeze(1) #shape:[3,4,1,5], 同 torch.squeeze(t,1)
unsqueeze:升维,比如 tensor 为[3x5], 那么执行 tensor.unsqueeze(0),变为[1x3x5]
沿着特定的维度重复这个张量,按照倍数扩充。既可以扩充维度,也可以重复添加元素。从右往左算,从最后的维度到最前的维度算。
x.repeat(a) x = torch.tensor([1,2,3,4]) x.repeat(3) //结果为:[1,2,3,4,1,2,3,4,1,2,3,4]
x.repeat(a,b) x = torch.tensor([1,2,3,4]) x.repeat(1,3) //结果为:[[ 1,2,3,4,1,2,3,4,1,2,3,4 ]] x = torch.tensor([[1,2,3],[4,5,6]]) x.repeat(2,3) //结果为:size=(4,9)
x.repeat(a,b,c) x = torch.tensor([1,2,3,4]) x.repeat(1,2,3) //结果为:[[[ 1,2,3,4,1,2,3,4,1,2,3,4 ],[ 1,2,3,4,1,2,3,4,1,2,3,4 ]]]
# mask中为0,则替换为value
a.masked_fill(mask==0, value=torch.tensor(-1e20))
对单一维度进行扩展,扩展的维度必须在最前面(第0维)
计算两个tensor之间乘积的函数,该函数要求两个tensor必须都是三维的,并且要求a,b两个tensor有如下格式:
a:(b,n,m)
b:(b,m,p)
则result = torch.bmm(a,b),维度为:(b,n,p)
其实这个三位张量的第一个维度就是batchsize,然后后面量维就是矩阵乘法了。
原型:torch.nn.functional.softmax(input, dim=None, _stacklevel=3, dtype=None)
dim参数来指定归一化的维度
softmax的理解,$s_i = \frac{e^i}{\sum \limits _j^n e^j}$
对于序列[1,2,3,4], 其softmax为:[0.0321, 0.0871, 0.2369, 0.6439]
可以知道数字越大,占比越多
torch.randn(5, 3, 10)
生成5组3x10个在0-1中符合正态分布的随机数
当调用contiguous()时,会强制拷贝一份tensor(即深拷贝),让它的布局和从头创建的一模一样,但是两个tensor完全没有联系
normal(mean, std, *, generator=None, out=None)
torch.normal(mean=0.,std=1.,size=(2,2)) #我们从一个标准正态分布N~(0,1),提取一个2x2的矩阵
还可以用矩阵。。
使用
https://zhuanlan.zhihu.com/p/415223758
torch.topk(tensor1, k=3, dim=1, largest=True)
* k #取的元素个数
* dim #选取的维度
* largest #从大到小取元素
* sorted #返回的结果按照顺序返回
* 返回值第一个为结果,第二个为结果的下标
例如:对一个2x3的矩阵
$\begin{bmatrix} 1&2&3 \ 4&5&6 \end{bmatrix}$
torch.topk(tenc, k=2, dim = 1, largest = True)
torch.topk(tenc, k=1, dim = 0, largest = True)
用于处理矩阵求和
例如:C = torch.einsum(“ijk->jk”, A) 即: $C_{jk}=\sum\limits_i A_{ijk}$
例如:C = torch.einsum(“ijm,ijk->jm”, A, B) 即: $C_{jm}=\sum\limits_i\sum\limits_k A_{ijm}*B_{ijk}$
公式是知道了,可以这么理解,矩阵的相乘可以表示为:einsum(“ab,bc->ac”,A,B),即A(ab),B(bc),结果为C(a*c)。以此类推可得此公式表示为张量乘法,不仅可以表示同维度,也可以表示不同维度的乘法。
https://blog.csdn.net/zhaohongfei_358/article/details/125273126
对张量的某个维度求和,从结果上来看,就是把对应的维度求和压缩成一个元素,其余结构保持不变。keepdim 则是表示是否保留这个压缩后的维度,相当于对这个维度做 squeeze 操作。
m = torch.randn([2,5,3]) #shape: [2,5,3]
m.sum(0) #shape: [5,3]
m.sum(0, keepdim = Ture) #shape: [1,5,3]
m.sum(1) #shape: [2,3]
m.sum(1, keepdim = Ture) #shape: [2,1,3]
两者都是将张量进行拼接,最后输出一个张量
#---cat---
#torch.cat(tensors, dim=d, *, out=None)
#tensors 可以是多个张量
#除了要进行cat的维度外,其余维度要和待拼接的tensor保持一致
input = torch.ones(1,2,5)
input2 = torch.ones(2,2,5)
output = torch.cat([input2, input,input],0)
print(output.shape) #shape [4,2,5]
#---stack---
#torch.stack(tensors, dim=d, *, out=None)
#沿新维度连接一系列张量,所有张量都需要具有相同的大小
input = torch.ones(1,2,5)
output = torch.stack([input, input,input],0) #在原来的0维前添加
print(output.shape) #shape: 3,1,2,5
output = torch.stack([input, input,input],2) #在原来的2维前添加
print(output.shape) #shape: 1,2,3,5
在 pytorch 的神经网络种,可学习的参数一般是在线性层 nn.Linear 中的权重和偏置,还有就是使用 nn.Parameter 定义的变量。
torch.nn.Parameter 是继承自 torch.Tensor 的子类,其主要作用是作为 nn.Module 中的可训练参数使用。它与 torch.Tensor 的区别就是 nn.Parameter 会自动被认为是 module 的可训练参数。nn.Parameter 中参数 requires_grad 默认值为 True,表示可训练,False 表示不可训练。
for name,param in rbf.named_parameters():
if param.requires_grad:
print("learned:",name)
torch.rand(sizes, out=None) #sizes为张量大小,01均匀分布
torch.randn(sizes, out=None) #标准正态分布
torch.randint(low=0, high, sizes, out=None) #区间分布
torch.Tensor(4,3,2) #生成 shape 为 [4,3,2] 的张量,值未经初始化,维度可继续增加
torch.empty(4,3,2) #生成 shape 为 [4,3,2] 的张量,值未经初始化,维度可继续增加
torch.zeros(4,3,2, dtype=None) #生成 shape 为 [4,3,2] 的张量,值为 0,维度可继续增加
torch.ones(4,3,2, dtype=None) #生成 shape 为 [4,3,2] 的张量,值为 1,维度可继续增加
torch.linspace(start,end,steps=100) #在start到end之间生成均匀分布的steps个数
torch.eye(n,m=None) #对角线为1,其余为0的矩阵。m默认等于n。
torch.full(sizes, fill_value) #生成size大小以fill_value填充张量
#Dataset是一个数据处理类。当我们继承了一个 Dataset类之后,我们需要重写 len 方法,getitem 方法
#接收一个索引,返回一个样本,和数组很像
#支持迭代,支持下标索引
from torch.utils.data import Dataset, DataLoader
class MyDataset(Dataset):
def __init__(self):
self.x = torch.linspace(1,10,10)
self.len = len(self.x)
#获取数据
def __getitem__(self, index):
return self.x[index]
def __len__(self):
return self.len
#DataLoader
torch.utils.data.DataLoader(
dataset, #需要提取数据的数据集,Dataset对象
batch_size=1, #每一次装载样本的个数
shuffle=None, #进行新一轮epoch时是否要重新洗牌,Boolean型
sampler=None,
batch_sampler=None,
num_workers=0, #是否多进程读取机制
collate_fn=None,
pin_memory=False,
drop_last=False, #当样本数不能被batchsize整除时, 是否舍弃最后一批数据
timeout=0,
worker_init_fn=None,
multiprocessing_context=None,
generator=None,
*,
prefetch_factor=2,
persistent_workers=False,
pin_memory_device='')
class MyDataset(Dataset):
def __init__(self):
self.x = torch.linspace(11,20,10)
self.y = torch.linspace(1,10,10)
self.len = len(self.x)
#获取数据
def __getitem__(self, index):
return self.x[index], self.y[index]
def __len__(self):
return self.len
mydataset = MyDataset()
mytrainload = DataLoader(dataset=mydataset,
batch_size = 5, #mydataset长度为:10/5
shuffle=False)
#遍历数据集
for step,(batch_x, batch_y) in enumerate(mytrainload):
print('step:', step,'| batch x: ', batch_x.numpy(), '| batch y: ', batch_y.numpy())
#输出数据
#step: 0 | batch x: [11. 12. 13. 14. 15.] | batch y: [1. 2. 3. 4. 5.]
#step: 1 | batch x: [16. 17. 18. 19. 20.] | batch y: [6. 7. 8. 9. 10.]
pytorch里面一切自定义操作基本上都是继承nn.Module类来实现的,我们在定义自已的网络的时候,需要继承nn.Module类,并重新实现构造函数__init__构造函数和forward这两个方法。
一般把网络中具有可学习参数的层(如全连接层、卷积层等)放在构造函数__init__()中,当然我也可以把不具有参数的层也放在里面。
一般把不具有可学习参数的层(如ReLU、dropout、BatchNormanation层)可放在构造函数中,也可不放在构造函数中,如果不放在构造函数__init__里面,则在forward方法里面可以使用nn.functional来代替。
forward方法是必须要重写的,它是实现模型的功能,实现各个层之间的连接关系的核心。
forward 中的参数怎么理解?x是一个参数列表?
一个普通的结构:将所有的层都放在了构造函数__init__里面,但是只是定义了一系列的层,各个层之间到底是什么连接关系并没有,而是在forward里面实现所有层的连接关系,如 参考
torch里面实现神经网络有两种方式
高层API方法:使用torch.nn.****来实现;
层API方法:使用低层函数方法,torch.nn.functional.****来实现;
原型: torch.nn.Linear(in_features, out_features, bias=True)
其实就是一个线性变换:$Y_{n*o} = X_{n*i}*W_{i*o} + b$ ,n 为输入向量的行数
例如:
input = torch.randn(5, 12) #相当于5个样本,每个样本12个特征
fc = nn.Linear(12, 15) #每个向量由12个特征, 输出15个特征
output = fc(input) #输出维度[5*15]
一共有四步
一、准备数据
对于输入的数据(以下为features)一定要做归一化,否会训练出来的loss回变成nan。
import pandas as pd
import numpy as np
import torch
from torch import nn
from torch.nn import functional as F
import matplotlib.pyplot as plt
import torch.utils.data as Data
import torch.optim as optim
from torch.nn import init
#二元数据
def prepare_data_2d():
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features=torch.tensor(np.random.normal(0,1,(num_examples,num_inputs)),dtype=torch.float)
labels=true_w[0]*features[:,0]+true_w[1]*features[:,1]+true_b
#加上一些非常小的波动
labels+=torch.tensor(np.random.normal(0,0.01,size=labels.size()),dtype=torch.float)
plt.plot(labels)
plt.show()
batch_size = 10
dataset = Data.TensorDataset(features, labels)
data_iter = Data.DataLoader(dataset, batch_size)
for X,y in data_iter:
print(X,y)
break
#一元数据,便于展示
def prepare_data():
num_inputs = 1
num_examples = 1000
true_w = 2
true_b = 4.2
#普通的线性函数:w*x + b
features=torch.tensor(np.linspace(1, num_examples,num_examples),dtype=torch.float)
labels=true_w*features[:]+true_b
#加上一些非常小的波动
labels+=torch.tensor(np.random.normal(0,1,size=labels.size()),dtype=torch.float)
plt.plot(labels)
plt.show()
batch_size = 10
dataset = Data.TensorDataset(features, labels) #特征和标签对应,即输入和输出
data_iter = Data.DataLoader(dataset, batch_size)
for X,y in data_iter:
print(X,y)
break
二、定义和初始化模型
class LinearNet(nn.Module):
def __init__(self,n_feature):
super(LinearNet,self).__init__()
self.linear=nn.Linear(n_feature,1)
#forward 定义前向传播
def forward(self,x):
y=self.linear(x)
return y
net=LinearNet(num_inputs)
init.normal_(net.linear.weight,mean=0,std=0.01)
init.constant_(net.linear.bias,val=0) #同:net.linear.bias.data.fill_(0)
#这里的net.linear指的是我们在LinearNet里面定义的,有些人会用net[0]
#查看网络结构
print(net)
#查看所有可学习的参数
for param in net.parameters():
print(param)
三、定义损失和优化算法
torch.optim模块提供了很多常用的优化算法比如SGD、Adam和RMSProp等。
#损失函数
loss=nn.MSELoss()
#优化器
optimizer=optim.SGD(net.parameters(),lr=0.03)
四、训练模型
#训练模型
for epoch in range(1, num_epochs + 1):
for X,y in data_iter:
output = net(X)
l = loss(output, y.view(-1,1))
optimizer.zero_grad()
l.backward()
optimizer.step()
print('epoch %d, loss: %f'%(epoch, l.item()))
dense=net.linear
print('true_w:',dense.weight)
print('true_b:',dense.bias)
是归一化的一种方法
均值为 0 方差为 1 的标准的正态分布的区间
nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, device=None, dtype=None)
参数:
normalized_shape:归一化的维度。如果只有一个值,则只会对最后一维进行归一化,且这个值必须和最后一维的值一样。若是两个值的数组,那么表示最后两个维度。以此类推。 比如,有shape为[2,3,4]的张量,若normalized_shape 为[4],则对最后一维做归一化;若normalized_shape为 [3,4],则对最后两维做归一化。
eps:加在方差上的数字,避免分母为0
比如,输入为(1, 3, 5, 5)的变量,并对其进行LayerNorm(想象有三层,每层是一个5*5的方块)。一般来说有两种归一化的方式, 如下,第一种归一化方法,对所有channel所有像素计算;第二种归一化方法,对所有channel的每个像素分别计算。
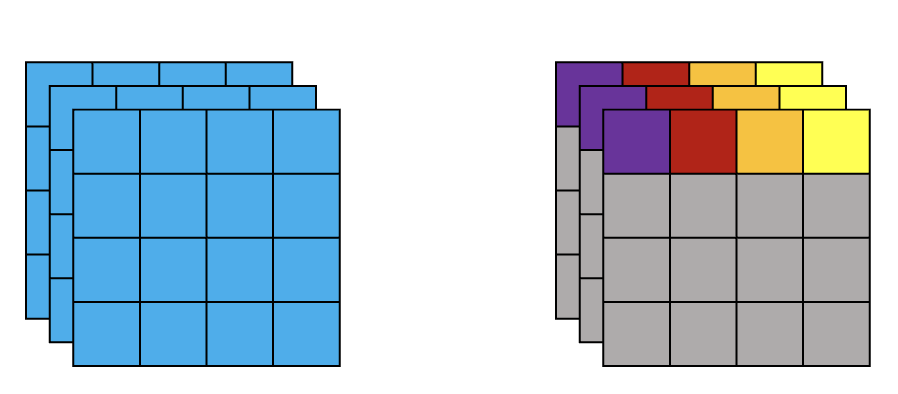
arr = np.arange(0,3*5*5).reshape(3,5,5)
arr = arr.astype(np.float32)
arr = torch.tensor(arr)
arr = arr.unsqueeze(0)
print(arr.shape)# shape: [1,3,5,5]
norm = nn.LayerNorm([3,5,5])
res = norm(arr)
print(res.shape) #shape: [1,3,5,5]
2.计算每个channel中的参数的均值和方差,然后归一化
arr = np.arange(0,3*5*5).reshape(3,5,5)
arr = arr.astype(np.float32)
arr = torch.tensor(arr)
arr = arr.unsqueeze(0)
print(arr.shape)# shape: [1,3,5,5]
arr = arr.permute(0,2,3,1).contiguous()
norm = nn.LayerNorm(3)
res = norm(arr)
print(res.shape) #shape: [1,5,5,3]
res = res.permute(0,3,1,2)
print(res)
https://blog.csdn.net/weixin_41978699/article/details/122778085
nn.Embedding(num_embeddings-词典长度,embedding_dim-向量维度)
表示输入的单词个数范围是在num_embeddings中(最多有这么多种单词),embedding_dim表示每个单词的向量长度。
embedding = nn.Embedding(10,3)
input = tensor.LongTensor([\[1,2,3,4],[5,6,7,8]])
embedding(input) #shape: [2,4,3]
torch.nn.Conv1d(in_channels, "输入的通道数"
out_channels, "卷积产生的通道数"
kernel_size, "卷积核的大小"
stride, "卷积的步幅。默认值:1"
padding, "添加到输入两侧的填充。默认值:0"
dilation, "内核元素之间的间距。默认值:1"
groups, "从输入通道到输出通道的阻塞连接数。默认值:1"
bias, "If True,向输出添加可学习的偏差。默认:True"
padding_mode "'zeros', 'reflect', 'replicate' 或 'circular'. 默认:'zeros'"
)
卷积后的维度:(n - k + 2 * p ) / s + 1 (k: 卷积核大小,p: 使用边界填充,s: 步长。)
每个卷积核与输入元素做乘积,然后计算和得到一个结果。见参考。
flowchart LR
i1 --> k1[i1 * k1] --> s1
i2 --> k2[i2 * k2] --> s1
i3 --> k3[i3 * k3] --> s1
i2 -.-> k1[i2 * k1] -.-> s2
i3 -.-> k2[i3 * k2] -.-> s2
i4 -.-> k3[i4 * k3] -.-> s2
...
import torch
import torch.nn as nn
input = torch.randn(1, 1, 5) #shape: [批大小, 数据的通道数, 数据长度]
conv = nn.Conv1d(in_channels=1, out_channels=1, kernel_size=3, stride=1, padding=0)
out = conv(input)
总的来说,这就是一个实现 MLP 结构的另一种方法
nn.Conv2d(in_channels=3,out_channels=64,kernel_size=4,stride=2,padding=1)
参考: https://blog.csdn.net/weixin_38481963/article/details/109924004
一个序列容器,用于搭建神经网络的模块被按照被传入构造器的顺序添加到nn.Sequential()容器中。除此之外,一个包含神经网络模块的OrderedDict也可以被传入nn.Sequential()容器中。
利用nn.Sequential()搭建好模型架构,模型前向传播时调用forward()方法,模型接收的输入首先被传入nn.Sequential()包含的第一个网络模块中。然后,第一个网络模块的输出传入第二个网络模块作为输入,按照顺序依次计算并传播,直到nn.Sequential()里的最后一个模块输出结果。
参考: https://blog.csdn.net/Just_do_myself/article/details/124195393
为了防止过拟合
class Dropout(nn.Module):
def __init__(self):
super(Dropout, self).__init__()
self.linear = nn.Linear(5,10)
self.dropout = nn.Dropout(p=0.3)
def forward(self, inputs):
out = self.linear(inputs)
out = self.dropout(out) #这里让上一层输出的30%的数据变为0
return out
def run():
net = Dropout()
inputs = np.arange(0,5)
inputs = torch.tensor(inputs, dtype=torch.float)
inputs = inputs.repeat(1,1)
print(inputs.shape)
print(net(inputs))
https://blog.csdn.net/weixin_47050107/article/details/122722516
#参数解释
#初始化
nn.RNN(
input_size, #输入的特征数
hidden_size, #隐层维度
num_layers = 1, #层数
batch_first = False, #把batch放在第一维度,即[batch, seq, feature]
nolinearity = 'tanh,
bias = 'True,
dropout = 0,
bidirectional = False,
)
#训练输入
def forward(self, x)
{}
# x 的 shape
# 1、对于没有batch,[seq_len, input_size]
# 2、对于 batch_first = False,[seq_len, batch_size, input_size]
# 3、对于 batch_first = True,[batch_size, seq_len, input_size]
#训练输出 shape
# 这里 d 是双向(是:2,否:1)
# 1、对于没有batch,[seq_len, d*hidden_size]
# 2、对于 batch_first = False,[seq_len, batch_size, d*hidden_size]
# 3、对于 batch_first = True,[batch_size, seq_len, d*hidden_size]
# 这里的 hidden_size 是隐层数量