↓跳到主要内容
  1. Blogs/
  2. 博客/

非平稳时间序列的预测

·1852 字·4 分钟·
学习笔记 深度学习 时间序列
目录

阅读基础：了解transformer的注意力机制，了解时间序列的稳定性

从本文你能了解到：如题，一种对非平稳时间序列预测的改进方法

本文来源：NIPS2022

背景介绍 #

我们知道，深度学习模型Transformer能够获取序列的特征，从而根据特征进行预测。

在时间序列中，有平稳时间序列和非平稳时间序列，简单来说平稳的时间序列就是序列均值和方差随着时间的增长变动不会太大。传统的ARIMA模型也是针对这种序列模型进行预测的。对于非平稳时间序列一般的做法也是将其转换为平稳时间序列，比如一阶或者二阶差分。

本文焦点 #

以往的研究主要采用平稳化的方法来减少原始序列的非平稳性，从而获得更好的可预测性。但是，被剥夺了固有非平稳性的平稳化序列对现实世界突发事件预测的指导意义不大。本文提出的时间序列预测框架既能处理平稳序列，又可以捕捉非平稳序列的特征。

本文贡献 #

  • 发现了非平稳时间序列的预测能力，以及现有平稳化方法造成的过平稳化问题。
  • 提出了Non-stationary Transformers 避免过平稳化的现象。
  • Non-stationary Transformers 在六个基准上，超过了四个现今主流的Transformer模型。

存在问题 #

问题背景 #

一开始对每一模型输入中的各个变量分别进行在时间维度的归一化，以消除了多变量时序数据中不同变量之间的尺度差异。另外，由于模型在训练阶段接收的输入是从整段序列上的各个滑动窗口采样得到，在时间维度上的进行窗口归一化实际上是针对各个输入进行的实例归一化（Instance Normalization），最终相邻窗口内的子序列都将服从相同的均值与方差，整体训练样本在时间维度上分布差异被减弱，从而提高了输入数据的平稳性。（也就是说，归一化也就是一种平稳化技术）

虽然增强了数据的可预测性，但也对原本的数据分布造成了不可逆转的退化。

在模型内部，尤其是用以捕捉时序依赖的注意力模块，依然得到的是经过平稳化后的输入，这也是Transformer学习到不易区分的注意力图的主要成因。

引出问题 #

  1. 如何设计可复原的平稳化
  2. 如何恢复原始的注意力（恢复归一化带来的分布信息损失）

Non-stationary Transformers架构 #

整体平稳化 #

  1. 问题引入

    首先，对每一模型输入中的各个变量分别进行在时间维度的归一化，以消除了多变量时序数据中不同变量之间的尺度差异。

  2. 问题分析和推理

    由于归一化的原因，整体训练样本在时间维度上分布差异被减弱，每个窗口的均值和方差变化都减弱了。因此在输入阶段中我们还存储了各个窗口内序列原本的均值和方差，在输出阶段中用这些统计量重新对模型的输出进行反向尺度变换，以恢复其归一化时丢失的分布信息。

  3. 改进和结果

    听起来很简单的样子，但是具体是如何实现的呢？ 就是输入序列减去均值，除以标准差，输出序列加上均值，乘上标准差。 由标准差：$\sigma _x$，均值：$\mu _x$， （两者维度都是C*1）,进行如下尺度变换：

    $$x’_i = \frac{1}{\sigma _x}\odot(x_i - \mu _x)$$

    在输出恢复原序列的非平稳信息 $$\hat{y}_{i}=\sigma_{\mathbf{x}} \odot(y_{i}^{\prime}+\mu_{\mathbf{x}})$$

注意力去平稳化 #

  1. 问题引入

    尽管反归一化模块在外部还原了时序数据部分的非平稳性，但在模型内部，尤其是用以捕捉时序依赖的注意力模块，依然得到的是经过平稳化后的输入。那么，如何捕捉到原始序列的注意力呢？

  2. 问题分析

    • 符号约定：S表示序列长度，C表示维度，k表示特征数，输入x就是S行C列。

    由于在归一化时存储了统计量，我们可以近似未归一化时原始输入，来得到的注意力图。

    去平稳化注意力

    $\mu_Q , \sigma_Q$ 都是k行一列, Q是S行k列。

    基于模型嵌入层（Embedding）和前向传播层（FFN）在时间维度的线性假设，并且由xi尺度变换和qi的计算方法，可以推断出Q’和K’（论文中附录A的证明）

    $$\mathbf{Q}^{\prime}=\frac{\left(\mathbf{Q}-\mathbf{1} \mu_{\mathbf{Q}}^{\top}\right)}{\sigma_{\mathbf{x}}}, \mathbf{K}^{\prime}=\frac{\left(\mathbf{K}-\mathbf{1} \mu_{\mathbf{K}}^{\top}\right)}{\sigma_{\mathbf{x}}}$$

    最后根据Softmax算子的平移不变性（就是所有元素加减常数后值不变），将上述上述公式带入原始注意力公式可简化为：

    $$Softmax\left(\frac{\mathbf{Q} \mathbf{K}^{\top}}{\sqrt{d_{k}}}\right)=>Softmax\left(\frac{\sigma_{x}^{2} \mathbf{Q}^{\prime} \mathbf{K}^{\top}+\mathbf{1} \mu_{\mathbf{Q}}^{\top} \mathbf{K}^{\top}}{\sqrt{d_{k}}}\right)$$

    引入了两个尺度变换因子（定义为去平稳化因子）：$\tau=\sigma_x^2, \Delta=K_{\mu Q}$

    • 这里不就又变成不平稳了吗？

      也不是变成了非平稳化，应该是即学习了平稳化的特征，又做出了非平稳化的相关变换。从架构图可以看到，平稳化后的序列经过了embedding，并且计算出了Q、K、V。

    平稳化注意力模块

    采用一个多层感知机，通过学习去平稳化因子，进而设计出去平稳化注意力模块。整体架构如下：

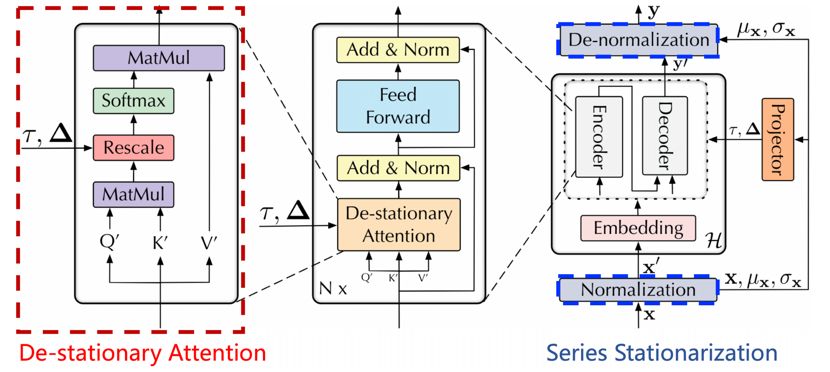
    ntransformerg

结果 #

在与时下最先进的深度时序预测模型的对比中，均取得了最优（SOTA）效果，特别是在在非平稳时序数据上，效果领先尤为明显。

启发和感想 #

  1. 时间序列只有平稳性和非平稳性这两种状况要考虑吗。总感觉这种做法就是对特别情况进行的一次特殊处理，不具有广泛性。

参考 #

https://blog.csdn.net/weixin_50810484/article/details/127788069

https://zhuanlan.zhihu.com/p/587665491

↑