- 🍊桔仔的博客/
- Blogs/
- 博客/
- Informer学习笔记/
Informer学习笔记
目录
针对人群：想深度学习最新方法进行时间序列预测的人
从本文你能了解到：注意力机制，transformer，informer
背景介绍 #
时间序列预测是什么 #
时间序列预测是指利用获得的数据按时间顺序排成序列，分析其变化方向和程度，从而对未来若干时期可能达到的水平进行推测。与其他回归问题的区别就是，时间序列自变量是时间，其变量结果与时间具有相关性。
目前的解决方案 #
目前的解决方案有以下三大类
-
传统时序建模
优点：
- 简单易用
局限：
- 只能针对平稳数据进行建模
- 只能处理单变量的预测问题
-
机器学习模型方法
优点：
- 计算速度快，模型精度高
- 可以解决大多数的复杂时序问题
局限：
- 需要较为复杂的人工特征过程部分，特征工程需要一定的专业知识或者丰富的想象力；
-
深度学习模型方法
优点：
- 模型可以自动学习特征工程，极大减少了人工；
局限：
- 需要较高的模型架构能力；
- 速度较慢；
细节如图：
flowchart LR
ts[时间序列预测]--> tra[传统经典时间序列预测方法]
tra --> ARIMA
tra --> Holt-Winters
tra --> FacebookProphet
ts --> ml[机器学习+特征工程]
ml--> gbm[GBM]
gbm --> AdaBoost
gbm --> GradientBoosting
gbm --> XGBoost
gbm --> LightGBM
ts --> dl[深度学习]
dl --> seq[Seq2Seq]
seq --> RNN,LSTM,DeepAR
dl --> cnn[CNN]
cnn --> WaveNet,TCN
dl --热门--> att[Attention]
att --> trans[Transformer]
att --> info[Informer]
att --> tft[TFT]
本文焦点 #
为了能够快速准确地预测具有复杂特征地时间序列，当前地研究重点都放在了利用深度学习来构建预测模型上。在众多地深度学习模型中，本文重点基于注意力机制的Informer模型在时间序列上的应用。 而Informer模型是在Transformer的基础上改进的，前者主要是针对后者的注意力机制和模型架构进行优化改进，大大提高了预测的效率，文章也将从这两个方面来进行说明。
存在问题 #
问题背景 #
Transformer之所以能够进行时间序列预测是因为其对序列数据具有很强的处理能力。2017年，Google的一篇 Attention Is All You Need 为我们带来了Transformer，其在NLP领域的重大成功展示了它对时序数据的强大建模能力，自然有人想要把Transformer应用到时序数据预测上。
在这之前的RNN在网络加深时存在梯度消失和梯度爆炸问题。即使是后续的LSTM ，在捕捉长期依赖上依然力不从心。这些已有的深度学习方法都无法适应长时间序列的预测，究其原因是其结构所具有的缺陷，导致了训练速度慢并且难以克服长时间训练的问题。而Transformer完全摈弃了这种循环网络架构，使用了自注意力机制和编解码结构，解决了已有模型的问题。
自注意力机制的优势
- 支持并行，训练得更快。基于RNN的模型中每一个隐状态都依赖于它前一步的隐状态，因此必须从前向后必须逐个计算，每一次都只能前进一步。而Transformer没有这样的约束，输入的序列被并行处理，由此带来更快的训练速度。
- 更强的长期依赖建模能力，在长序列上效果更好。在前面提到过，基于RNN的方法面对长序列时无法完全消除梯度消失和梯度爆炸的问题，而Transformer架构则可以解决这个问题
- Transformer可以同时建模长期依赖和短期依赖。Multi-head Attention中不同的head可以关注不同的模式。
- Transformer的AttentionScore可以提供一定的可解释性。通过可视化AttentionScore可以看到当前预测对历史值注意力的分布。
上面我例举出了使用了注意力机制具有的优势，以及解决的问题，那么这种即使是如何运作的呢？以下我将进行简单说明。
什么是注意力机制
自注意力就是计算节点两两之间的相关性。是一个序列到序列的操作，其中输入和输出都是相同的维度。评价注意程度（即两个向量的相似程度）可以用点积来表示。所以可以训练一个特征模型，构建特征的相关性。
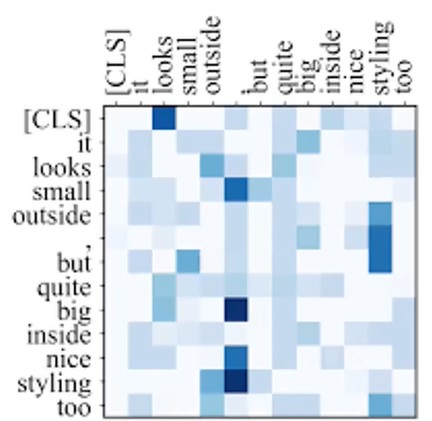
由于注意力机制有一定的可解释性，所以很容易将其可视化，如下：
这个图片是语言序列中表示两两单词的注意力，这里只展示一个单词的注意力。
注意力机制的工作方式
由于注意力计算的输入和输出维度都相同。为什么相同？
例如：
有输入编码序列：x1，x2，…，xt，输出序列：**y1，y2，…，yt，**对于每个点都有k个特征（k行一列）
注意力计算，两个点的 注意力分数 。
$$w’_{ij} = x^T_ix_j$$
这样理解，比如每个人都有一个喜好向量，对每个人的向量两两相乘，那么对于有相同兴趣的乘积就会大，两者 注意力分数 就高。
标准化： $$w_{ij}=\frac{w’_{ij}}{\sum_jw’ _{ij}}$$
wij 表示第 i 个点与第 j 个点的 注意力分数 。
第 i 个输出，关注所有输入点。
$$y_i = \sum\limits_jw_{ij}x_j$$
什么是QKV？为什么要QKV？
对于每个xi，它有三个作用：
- 与其他所有向量进行比较，以确定其自身输出 yi 的权重
- 与其他所有向量进行比较，以确定第 j 个向量 yj 的输出的权重
- 一旦建立了权重，它就被用作加权和的一部分来计算每个输出向量（用于预测）
上面直接建立注意力之间的关系，但是这种关系不够灵活，为了构建一个可控性比较强的输入，建立三个 k*k 的权重矩阵，对xi进行线性变换。
$$q_i = W_q x_i$$
$$k_i = W_k x_i$$
$$v_i = W_v x_i$$
（This gives the self-attention layer some controllable parameters, and allows it to modify the incoming vectors to suit the three roles they must play.[2]）
$$w’_{ij} = q^T_i k_j$$
$$w_{ij} = softmax(w’_{ij})$$
$$y_i = \sum_jw_{ij}v_j$$
即：$A(Q,K,V) = Softmax(\frac{QK^T}{\sqrt d})V$
除以一个开方d，可以防止数据太大，是因为softmax对很大的数据很敏感，这会降低学习效率。
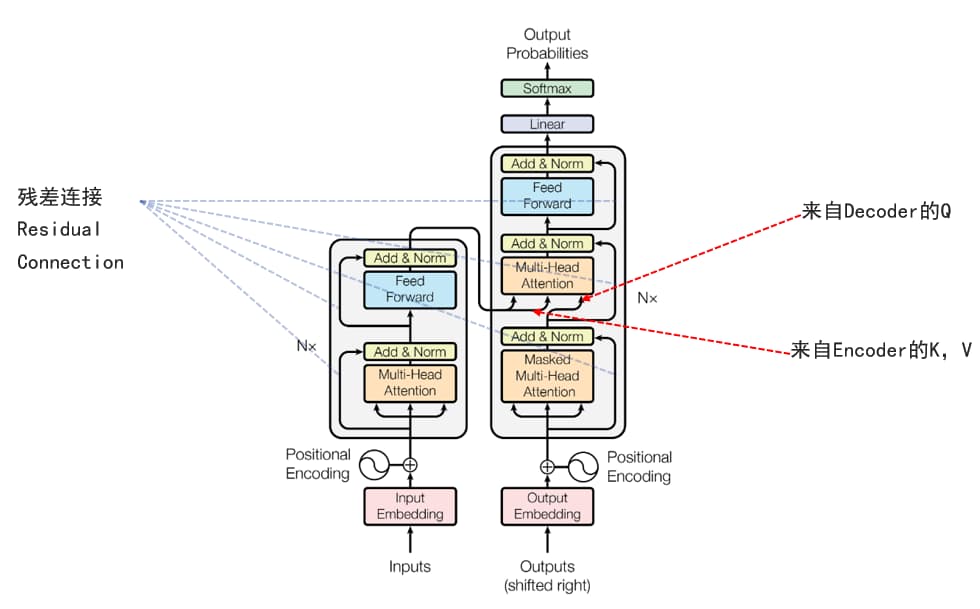
Transformer整体架构
讲完了注意力机制，然后再从整体架构的宏观层面来探究其运作过程。
分为Encoder和Decoder两部分，其中Encoder输出Q、K，Decoder输入V。
引出问题 #
上面对Transformer模型进行了简单的介绍，以及它所改进的问题，那么其真的就是完美无缺了吗？当然不是,再完美的模型肯定也有漏洞吧，不然怎么水论文🤭！大量研究发现了这个模型的一些缺点：
- 计算时间复杂度高：对于序列处理，会计算每个点与其他点的注意力，每一层的复杂度都是O(L^2)。
- 空间复杂度高：序列输入需要O(L^2)的空间复杂度
- 预测速度慢：对于序列输出，Decoder是一个个生成的
Informer架构 #
虽然Transformer 具有提高预测能力的潜力，但以上的问题使其无法直接应用于 LSTF，于是就有了Informer这个模型架构。Informer的主要改进有以下三点：
改进一：ProbSparse自注意力机制 #
-
问题引入
$$A(Q,K,V) = Softmax(\frac{QK^T}{\sqrt d})V$$
Transformer结构中这个公式括号里面的分子计算就是平方时间复杂度的罪魁祸首，这个公式是要算出输入序列的自注意力。那么它是否有优化空间呢，这篇论文给出了答案。
-
分析问题
-
推论和验证方法
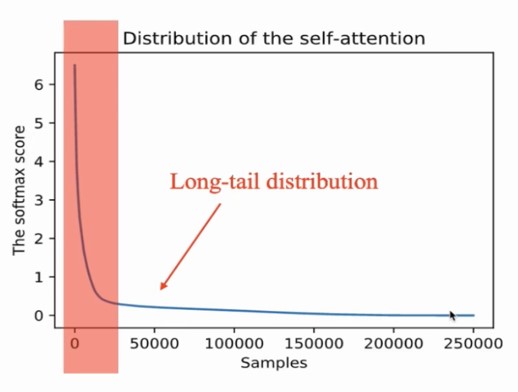
首先，由于注意力机制提供了一定的可解释性，作者对其进行了可视化操作，发现了注意力矩阵是个稀疏矩阵，并且这个“稀疏”的自注意力分数形成一个长尾分布。
作者将此公式进行一个变换，转换成一个概率分布的公式，如下：
$$A(q_i, K, V) = \sum \limits _j \frac{k(q_i, k_j)}{\sum l k(q_i, k_l)} v_j = E{p(k_j|q_i)}$$
由于变换成了概率分布，那么就可以用KL散度对这个分布进行评估。直观理解就是：散度越大，意味着attention的概率和均值概率的差越大，注意力越强。
最后发现这是一个LSE问题，可近似取最大值，则有以下变换：
$$M(q_i, K) = max_j{\frac{q_i k_k^T}{\sqrt d}} - \frac{1}{L_K}\sum ^{L_K}_{j=1} \frac{q_i k_k^T}{\sqrt d}$$
-
改进和创新结果
以上推理只是严格的数学证明，并没有在代码中体现出来，而代码的主要设计其实很简单：
首先对K进行随机采样（采样c*log（L）个），得到K_sample，对每个 qi∈Q 关于K_sample求M值。因为基于以上的发现和推理，这样处理足以拟合原始的分布。
-
改进二：蒸馏操作 #
-
问题引入
编码器旨在提取长序列输入的稳健的远程依赖关系。空间复杂度高，注意力矩阵大小为L^2。
-
分析问题
-
推论和验证方法
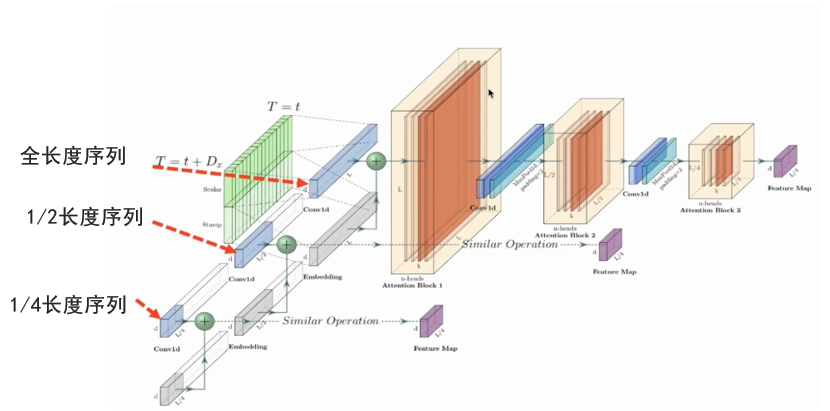
空间复杂度高无非就是要减少空间嘛，那么只要在每一层进行一次一维卷积降采样，空间复杂度不就降下来了（只保留了最后一个小矩阵）。但是这样可能会带来一些特征损失，所以作者为了增强其鲁棒性，增加了几个小于主序列长度的次序列， 得到了多个feature map，最后将其拼接起来。
-
改进和创新结果
-
改进三：生成式解码器 #
-
问题引入
对于序列输出，Decoder是一个个生成的，每次只预测了一个点，这样导致逐步推理与基于 RNN 的模型一样慢。
-
分析问题
-
推论和验证方法
按照NLP中的start token，拓展这个概念，针对长序列，一次性生成所有数据从长序列中采样一个 Ltoken 的输出序列之前的片段，与 0 拼接，输入decoder。也就是说，比如一次性预测的decoder的输入有72个点，前面48个是已经预测出来的，后面的是0填充的，那么我们用前面48个点带后面24个点，就一次预测了24个点，输出长度就是72（48个老司机带24个小司机🚗），而不是“逐步”的方式预测长序列序列，这极大地提高了长序列预测的推理速度。
-
改进和创新
-
结果 #
作者的结果不仅速度提高了，而且效果还比其他模型要好。这个结果值得商榷，有可能是作者对数据进行了优化。
参考 #
[1]（2017-12-05）Attention Is All You Need http://arxiv.org/abs/1706.03762
[2]（2019-08-18）https://peterbloem.nl/blog/transformers
[3] Halfling Wizard.（2021） [OL]Attention Is All You Need - Paper Explained https://www.youtube.com/watch?v=XowwKOAWYoQ
[4]（2021-05-18）Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting https://ojs.aaai.org/index.php/AAAI/article/view/17325
[5] 张帅.（2021-03-24）第55期 - AAAI 2021最佳论文 | Informer：比Transformer更有效的长时间序列预测方法 https://www.bilibili.com/video/BV1rb4y1Q7SJ/?spm_id_from=333.337.search-card.all.click&vd_source=be64fb00ff66079e029634bb4dd1f1bf
[6] （2021-6）https://zhuanlan.zhihu.com/p/374936725